I will post from time to time about the model that I have built to simulate and project Premier League matches. Whenever I do this I get asked about how it works, this post will go through I how I do things, trying to explain my decision-making along the way.
I don’t think that this is a perfect model by any stretch of my imagination (for example I would not use this to bet blindly but have made profitable bets informed by this plus my other knowledge) but I do think that it is directionally right and helps to give an idea of the realistic range of outcomes. Plus it allows for me to play around with different scenarios to gauge how that might move odds.
Rating Teams
The first step in my model is establishing an overall rating for each team. There are lots of ways that you can go about doing this but I think the simplest method with the most bang for your buck is looking at simply Goals and Expected Goals. These make up the biggest portion of a team’s rating.
Goals are weighted at 30% and Expected Goals (from Opta via FBRef) are 70%. I do this because both provide vital information about a team and combining them makes for a better picture rather than looking at each individually.
For these, there is a variable weighting to take my main three inputs (weighted current season, weighted previous season, and last 10 matches) and combine them into one number. For the weighting of the matches I use an exponential decay that looks at the time in weeks from when that match took place to today.
For this the equation is 0.96^(weeks since played) to determine the weighting for that match. This makes it so the most recent matches count more heavily
This is used for both the current season and the previous season, while last 10 matches played is left unadjusted.
Other factors
Next was looking at a team’s wages. I have looked into this and wages tell a very compelling story for how well a team will do in the coming season.
This is stronger than something like transfer spending which can be very noisy and still ultimately ties into wages. The big issue is that wage data is not great but this is now posted on FBRef so my hope is that this is all hopefully wrong in the same way that cancels things out.
Lastly and maybe this is a bit of a cheat, I also look at the betting odds over/under for each team. The collective wisdom of people risking their money has a good track record and I think that this would certainly help to capture information that might not be knowable through goals or wages.
Combining factors
The last step for creating the team rating is to weight everything and have it spit out a rating. This is another weighting scheme that changes over the course of the season.
At the start of the season, last season’s results are the biggest factor with 55% of the weight, with betting odds and wages combining equally for the remaining 45%.
As the season progresses the current season becomes more and more important.
At the 10 matches played point the weighting looks like this: Last season 31%, Current season 28%, Betting odds 26%, Wages 15%.
At the 14 matches played mark, the current season becomes the biggest factor, Last season 20%, Current season weighted 33%, Last 10 matches 20%, Betting odds 17%, Wages 10%.
This gets stronger as the season progresses but the previous information never fully goes away as a factor.
One of the new wrinkles I am considering is looking at something for making an adjustment for January transfer spending, I will probably think on this for a while but I do think trying to capture that without having to wait the 7-10 matches for it to filter in would be nice. - This will be updated if this happens.
Creating Match Odds
The next step is creating match odds. To do this I take the team ratings and combine them into a projection for the number of goals scored for each team. For this I decided the way I wanted to do things was to keep things simple, I simply take the attack rating for one team, add the defense rating for the other team, divide by 2 and then multiply by a home-field advantage factor (right now I have both a 5% bonus and 5% penalty).
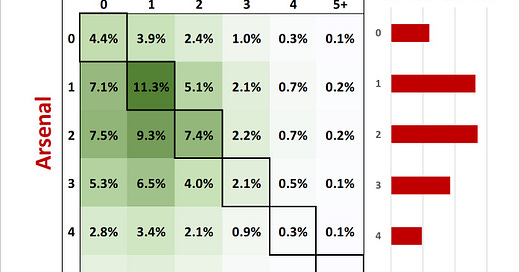
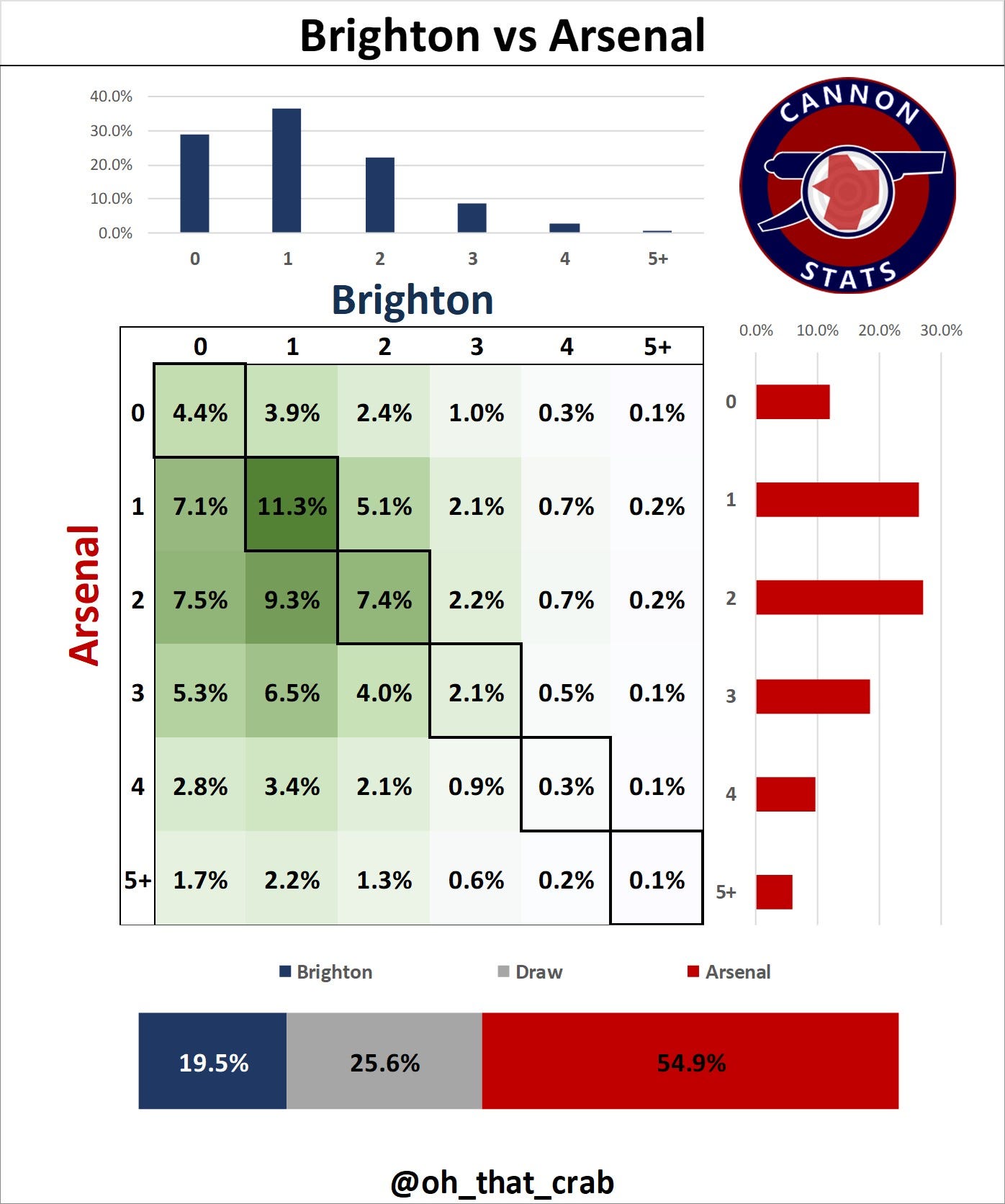
The next step is taking these expected goal figures and putting them into Poisson distributions to model the probability of certain amounts of goals being scored. Doing this for both teams then allows you to figure out the odds for each scoreline and thus the odds of a win/loss/draw. That is how this graphic is derived.
I do this exercise for each match to get the match odds. From there we take these match odds and simulate a season.
Simulating a season
Simulating a season is a big Monte Carlo simulation that runs things 10,000 times.
I have the ability to run my model hot or static. I will almost always choose to run it hot, the difference is that in the hot model the simulated outcome of the match before is used to change the team ratings and odds for all subsequent matches. This more closely matches what happens in real life.
To simulate a match I simply generate a random number between 0 and 1, take the probability distribution from the match odds for the goals and use that to determine the goals scored for each team. The goals are compared and that gives the outcome of the match for win, loss, or draw with these being recorded to be used at the end.
To simulate a season I would do this same thing for each match, record the number of goals for and against, the number of wins, losses and draws, the points and where a team finished and save that. Then I would start again simulating the season 10,000 times.
After all of that, I am able to get information like this:
So this is how my simulation model works.
Could you make a fancier one? Yes, you can, but for me the added complexity for in my view small gains in accuracy aren’t worth it for how I use it.
Could you make a more accurate one? Yeah, I am certain that there are more advanced models, specifically ones built for gambling out there that take into account more information and are more accurate. It is again the trade-off in time building and computing power to run.
Does this mostly work and point me in the right direction without implicitly introducing bias? Yes, I think it does and that is why I do it.
Let me know if you have any questions about how this works in the comments (open for everyone this time).






This is a fabulous walk through of your process!
Brilliant, Scott. I love the expression that 'no model's perfect, but some are informative', and I definitely think yours provides a lot of important info. Good explanation at the end re added complexity perhaps not being worth the time/effort.
The thing that concerns me most with the models on Arsenal's increasingly high odds of winning the league (ie, 50% on fivethirtyeight) is the possibility that things just fall apart after an injury to any of a few key players...I don't think City suffers from that downside as much, though KDB or Haaland going down wouldn't help. Saka/Martinelli/Odegaard/#5 go down, and I think our odds drop by 5-10 percentage points. I still think something similar with Jesus that hasn't yet been reflected in the models. (I have no empirical evidence, just my feeling which I'd love to prove/disprove)
Anyway, I think this falls in the category of the 'added complexity isn't worth the marginal gains', but the fact that City is the only club with two top tier 11s whereas we can only pray to the injury gods is an important differentiator that protects City's downside. Maybe there's an easy way to capture 'percent of team salary that is expected to be out with injury in the next few games'? That would reflect the injuries that already happened and expected downside to result. There would also be the more complex measure that shows the difference in value between the starter and backup (and likelihood of injury to starter), which would reflect downside. Again, all this is likely not worth the effort, but I still have ptsd after last season, so yeah.
Other factors that would be easier to implement and that I think matter relate to how many days of rest teams have - I think 3 vs 4 days is an important distinction that I don't think models capture. Again, maybe I'm just thinking of anecdotal evidence, but coaches often complain about the lack of rest between games being a disadvantage, so I'm guessing it's a factor.
Thanks again for your work on this. Some very cool stuff!